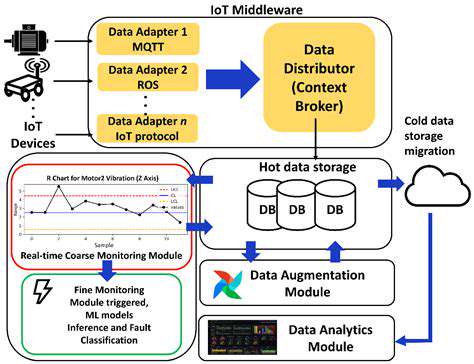
Pauli-X Gate (NOT Gate)
In quantum computing, the Pauli-X gate (denoted as X or σx) serves as the quantum equivalent of a classical NOT gate. This gate performs a crucial bit-flip operation, transforming |0⟩ to |1⟩ and vice versa. Such phase inversion forms the bedrock of quantum state manipulation, enabling the construction of sophisticated quantum algorithms.
The mathematical representation of this gate as a 2×2 matrix reveals its fundamental operation. When applied to a qubit's state vector, it produces the characteristic state inversion. Mastering this matrix representation provides deep insight into the quantum mechanical principles governing qubit behavior, which proves essential for practical quantum computing applications.
Pauli-Y Gate
Represented by Y or σy, the Pauli-Y gate introduces a complex phase transformation rather than a simple state flip. It maps |0⟩ to i|1⟩ and |1⟩ to -i|0⟩, creating a 90-degree phase shift that enables nuanced quantum state manipulation. This phase modification capability becomes particularly valuable when constructing quantum circuits requiring precise phase control.
While the operation might appear subtle, its implications are profound. The gate's ability to alter phase without changing state probabilities makes it indispensable for creating quantum interference effects, a phenomenon that underpins many quantum algorithms' superior performance.
Pauli-Z Gate
The Pauli-Z gate (Z or σz) specializes in phase manipulation, leaving |0⟩ unchanged while applying a -1 phase factor to |1⟩. This selective phase flipping becomes crucial when working with quantum superposition states and entanglement. The gate's operation reveals the intricate relationship between quantum states and their phase components.
In practical applications, the Pauli-Z gate proves essential for quantum error correction and various quantum algorithms. Its phase manipulation capability allows researchers to create controlled interference patterns between quantum states, enabling computations that would be impossible on classical systems.
Single-Qubit Gates: Beyond the Pauli Gates
Single-Qubit Gates: A Deeper Dive
Single-qubit operations form the foundation of quantum circuit design. These fundamental transformations enable state preparation, manipulation, and measurement - the essential operations in any quantum algorithm. Their proper understanding separates effective quantum programmers from mere users of quantum computing frameworks.
Hadamard Gate: Superposition Pioneer
The Hadamard gate's ability to create equal superpositions from basis states makes it perhaps the most frequently used gate in quantum algorithms. By transforming |0⟩ into (|0⟩ + |1⟩)/√2, it enables the quantum parallelism that gives quantum computing its potential advantage.
Phase Gates: Subtle but Powerful
Phase gates (S and T gates) operate by introducing precise phase shifts to quantum states. While these changes don't affect measurement probabilities directly, they critically influence quantum interference patterns that form the basis of many quantum algorithms' computational advantages.
Rotation Gates: Precision in Quantum Control
RX, RY, and RZ gates provide arbitrary angle rotations around their respective Bloch sphere axes. This fine-grained control enables exact state preparation and forms the basis for variational quantum algorithms that may prove crucial for near-term quantum applications.
Two-Qubit Gates: Entanglement and Control
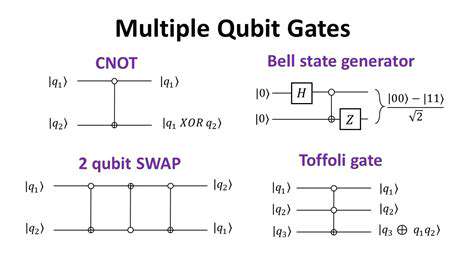
Entanglement Creation and Manipulation
Two-qubit operations enable the creation of entangled states that exhibit non-classical correlations. The CNOT gate, serving as the quantum equivalent of a classical controlled operation, forms the workhorse of entangling operations in most quantum circuits.
Quantum Algorithm Implementation
Advanced gates like the SWAP and controlled-phase gates expand the toolkit available for algorithm design. These operations enable more efficient implementations of quantum algorithms while potentially reducing circuit depth and error susceptibility.
Quantum Circuit Construction and Applications
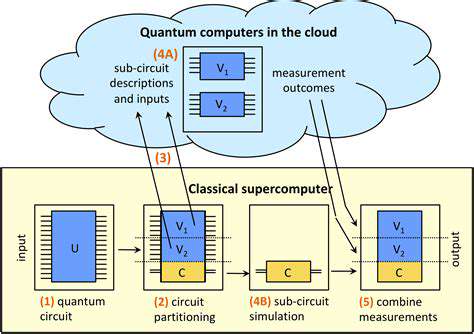
Circuit Optimization Techniques
Effective quantum programming requires careful attention to circuit optimization. Techniques like gate cancellation, commutation rules, and specialized compilation methods can significantly reduce resource requirements while maintaining computational accuracy.
Error Mitigation Strategies
Current quantum hardware necessitates sophisticated error mitigation approaches. Methods like zero-noise extrapolation and probabilistic error cancellation have shown promise in extending the capabilities of noisy intermediate-scale quantum devices.