Quantum Error Correction: A Necessary Component
Quantum Error Correction: The Foundation
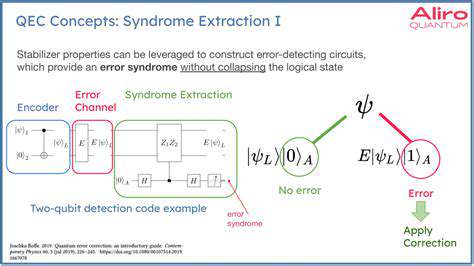
Quantum computers promise unparalleled computational power, but their delicate quantum states are incredibly susceptible to errors. These errors, stemming from interactions with the environment, can quickly corrupt the fragile quantum information, rendering calculations inaccurate. This inherent instability necessitates the development of robust error correction techniques, crucial for realizing the full potential of quantum computing. Quantum error correction is not merely a desirable feature; it's a fundamental requirement for building practical quantum computers.
The principles behind quantum error correction are rooted in the ability to detect and correct these errors without disturbing the quantum information too much. This is achieved through the creation of redundant quantum information encoded in multiple qubits. By carefully manipulating these redundant qubits, quantum error correction codes can identify and counteract errors, ensuring the integrity of the computation.
Quantum Error Correction Codes: Different Approaches
Various quantum error correction codes exist, each tailored to specific error types and qubit architectures. These codes differ in their complexity, error correction capabilities, and the number of qubits they can protect. Some prominent examples include the Shor code, the Steane code, and the surface code, each with its own strengths and weaknesses. The choice of code often depends on the specific challenges posed by the quantum hardware.
Understanding the strengths and weaknesses of each code is critical for selecting the most appropriate approach for a given quantum computation. Factors like the error rate of the qubit system, the desired fault tolerance, and the computational overhead associated with the code are crucial considerations in the selection process. The field is actively evolving, with researchers constantly developing and optimizing new quantum error correction codes.
Implementation Challenges and Future Directions
Despite significant theoretical progress, implementing quantum error correction in real-world quantum computers presents considerable challenges. Building hardware capable of maintaining the necessary coherence and control over numerous qubits is a significant hurdle. Furthermore, the overhead of error correction can significantly impact computational resources and speed. This necessitates ongoing research into more efficient and scalable error correction methods.
Future research in quantum error correction aims at developing more robust codes that can tolerate higher error rates, minimizing the overhead associated with error correction, and integrating error correction into the design of quantum hardware. Researchers are actively exploring novel approaches to error mitigation and hardware enhancements to minimize the impact of environmental noise and imperfections on quantum computations.
The Role of Quantum Error Correction in Quantum Computing
Quantum error correction is not just a technical detail; it's the cornerstone of building reliable and scalable quantum computers. Without robust error correction, the inherent fragility of quantum states would severely limit the size and complexity of quantum computations. The development of effective quantum error correction methods is crucial for realizing the transformative potential of quantum computing in various fields, from drug discovery to materials science to cryptography.
This technology lays the groundwork for performing complex calculations that are impossible on classical computers, opening up entirely new avenues of scientific discovery and technological advancement. The ongoing pursuit of more sophisticated error correction techniques is vital for the future of quantum computing.
Quantum Algorithm Development: The Software Side of the Equation
Quantum Algorithm Design Principles
Developing quantum algorithms requires a unique approach that leverages the principles of quantum mechanics. This involves understanding the fundamental concepts of superposition and entanglement, which are crucial for exploiting the computational power of quantum systems. Quantum algorithms often differ significantly from their classical counterparts, demanding a shift in thinking about problem representation and solution strategies. A thorough understanding of these principles is paramount for successful quantum algorithm design.
Quantum Circuit Construction
Quantum algorithms are implemented as sequences of quantum gates, forming quantum circuits. These circuits manipulate qubits, the fundamental units of quantum information, through unitary transformations. Understanding how to combine various quantum gates to achieve desired transformations is a crucial skill in quantum algorithm development. Careful consideration of gate sequences is vital to ensure the efficient and accurate execution of the algorithm.
Qubit Encoding and Manipulation
The encoding of classical information onto qubits is a critical step in quantum algorithm design. Choosing appropriate qubit representations and implementing efficient techniques for manipulating these qubits are essential for successful algorithm implementation. This includes understanding the nuances of different qubit types and their interactions within the quantum system. Proper qubit encoding and manipulation directly influence the performance and accuracy of quantum algorithms.
Error Mitigation and Quantum Noise
Quantum computers are susceptible to errors due to various sources of noise. Implementing strategies for mitigating these errors is crucial for achieving reliable and accurate results. These strategies include techniques like error correction codes and noise-mitigation algorithms. Minimizing the impact of noise is a key challenge in scaling quantum computation. Careful consideration of error sources and the implementation of appropriate mitigation techniques are vital.
Quantum Algorithm Analysis and Efficiency
Analyzing the efficiency of quantum algorithms is an essential aspect of quantum algorithm development. Metrics such as quantum speedups and resource requirements are critical for evaluating the performance of an algorithm. This analysis helps in identifying potential bottlenecks and optimizing algorithms for specific quantum hardware architectures. Understanding the resource requirements, such as qubit counts and gate counts, is essential for predicting the feasibility of implementing a given algorithm.
Quantum Simulation and Benchmarking
Quantum simulation is a powerful application of quantum algorithms. It enables the modeling of quantum systems, which is crucial for understanding and predicting their behavior. Developing quantum simulations requires expertise in both quantum mechanics and computational techniques. The development of robust benchmarking strategies is essential for evaluating the performance of quantum algorithms. This ensures that algorithms are well-suited for their intended application in quantum computing.
Quantum Algorithm Libraries and Tools
The availability of quantum algorithm libraries and tools is essential for accelerating the development process. These tools often provide pre-built modules and functions for common quantum computations. Leveraging these resources can significantly streamline the development process and allow researchers to focus on the specific problem domain. The use of quantum computing libraries allows for rapid prototyping and experimentation with different quantum algorithms. This facilitates the development of novel and efficient solutions.