Introduction to Supervised Learning for Regression
Understanding Regression Problems
Supervised learning, a cornerstone of machine learning, encompasses various techniques for building models that predict outcomes based on input data. Regression, a specific type of supervised learning, focuses on predicting continuous numerical values. Imagine trying to forecast house prices based on factors like size, location, and number of bedrooms. This is a regression problem, where the goal is to develop a model that maps these input features to a continuous output—the house price. Understanding the nature of the problem and the expected output is crucial for choosing the right regression model and evaluating its performance.
Regression models aim to establish a relationship between input variables (predictors) and a continuous target variable. This relationship can be linear, non-linear, or even complex. The key is to find the best-fitting function that minimizes the difference between the predicted and actual values. This process of finding the optimal model is a critical aspect of regression modeling, and it involves various statistical techniques and algorithms.
Key Concepts in Regression Modeling
Several key concepts underpin regression modeling. One fundamental concept is the idea of minimizing error. Regression algorithms strive to find the model that produces the smallest difference between the predicted and actual values. This difference is often measured using metrics like Mean Squared Error (MSE) or Root Mean Squared Error (RMSE). Understanding these metrics is essential for evaluating the performance of a regression model and comparing different models.
Another important concept is feature selection. The input variables, or features, used in a regression model can significantly impact the model's performance. Choosing the right features and understanding their relationship with the target variable is crucial for building an accurate and reliable model. Carefully selecting features can greatly enhance the model's predictive power and reduce overfitting.
Types of Regression Models and Their Applications
Several different regression models exist, each with its strengths and weaknesses. Linear regression, a fundamental approach, assumes a linear relationship between the input features and the target variable. Its simplicity and ease of interpretation make it a popular choice for initial analyses. However, its limitations in capturing complex relationships have led to the development of more sophisticated models.
Beyond linear regression, other models like polynomial regression, support vector regression, and decision tree regression offer greater flexibility in modeling complex relationships between variables. Choosing the appropriate model depends on the specific characteristics of the dataset and the nature of the relationship between the input and output variables. For instance, polynomial regression can handle non-linear relationships, while support vector regression is particularly useful for high-dimensional data. Understanding the strengths and weaknesses of each model is crucial for selecting the most suitable approach for a given regression problem.
Key Concepts in Regression Analysis

Understanding the Fundamentals
Regression analysis is a powerful statistical method used to model the relationship between a dependent variable and one or more independent variables. It's crucial in various fields, from economics and finance to healthcare and engineering, enabling researchers and analysts to understand how changes in independent variables affect the dependent variable. This understanding is vital for making predictions and informed decisions. The goal is to establish a mathematical equation that best describes this relationship, allowing us to estimate the dependent variable's value based on known or predicted values of the independent variables.
A core concept is the concept of a linear relationship. While regression models can be non-linear, the most basic form assumes a straight-line relationship between the variables. Understanding the linearity assumption is critical for interpreting the results accurately. Linear regression models are often easier to interpret and implement than more complex models. Furthermore, the underlying assumptions of regression analysis, such as the independence of errors and the normality of residuals, are crucial for ensuring the validity of the conclusions derived from the analysis.
Interpreting Regression Coefficients
Regression coefficients represent the change in the dependent variable for a one-unit change in the corresponding independent variable, holding all other independent variables constant. This allows us to quantify the impact of each independent variable on the dependent variable. Understanding these coefficients is crucial for drawing meaningful insights from the analysis. Proper interpretation of these coefficients is essential for accurately assessing the relationships within a dataset.
For instance, a positive coefficient indicates a positive relationship, meaning that an increase in the independent variable is associated with an increase in the dependent variable. Conversely, a negative coefficient signifies an inverse relationship, where an increase in the independent variable is associated with a decrease in the dependent variable. Careful consideration of the signs and magnitudes of coefficients provides valuable insights into the nature and strength of these relationships.
Evaluating Model Fit and Significance
Model fit refers to how well the regression model explains the variation in the dependent variable. Several metrics, such as R-squared, assess this fit. A higher R-squared indicates a better fit, meaning the independent variables explain a larger proportion of the variance in the dependent variable. Understanding how well the model fits the data is crucial for ensuring the model's reliability in making accurate predictions. A good fit is essential for drawing meaningful conclusions from the analysis.
Furthermore, statistical significance tests assess whether the observed relationships between variables are likely due to chance or are truly meaningful. These tests, such as t-tests or F-tests, help determine whether the coefficients are statistically different from zero. Understanding the significance of the coefficients is paramount to determining the validity of the model's conclusions. Without this, the analysis might be misleading or inaccurate. A lack of statistical significance suggests that any observed relationship might be spurious.
These key concepts—fundamental understanding, coefficient interpretation, and model evaluation—are essential for conducting reliable and insightful regression analysis.
Model Evaluation and Selection
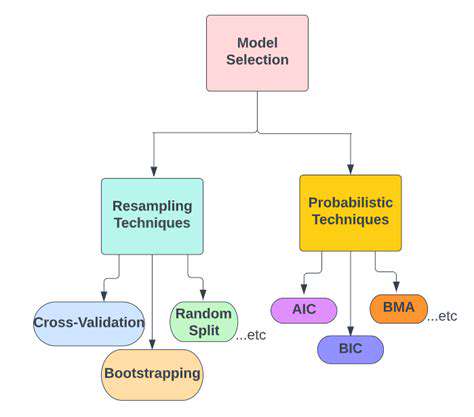
Model Performance Metrics
Evaluating the performance of a machine learning model is crucial for selecting the best-performing model for a given task. Different types of models excel at different tasks, and choosing the right model often depends on the specific metrics used to assess its performance. Understanding these metrics, such as accuracy, precision, recall, and F1-score, is essential for making informed decisions. Accuracy, while a commonly used metric, may not be sufficient for all scenarios, as it can be misleading when dealing with imbalanced datasets.
Precision and recall provide a more nuanced understanding of a model's performance, particularly useful in scenarios where false positives or false negatives are costly. For example, in medical diagnosis, a high false positive rate could lead to unnecessary treatments, while a high false negative rate could result in missed diagnoses. Precision measures the proportion of correctly predicted positive instances out of all predicted positives, while recall measures the proportion of correctly predicted positives out of all actual positives.
Model Selection Strategies
Choosing the right model for a specific task involves careful consideration of various factors, including the nature of the data, the complexity of the task, and the available computational resources. Different model selection strategies exist, such as cross-validation, which helps to estimate the generalization performance of a model on unseen data.
Techniques like grid search or randomized search can be employed to find the optimal hyperparameters for a given model. These techniques systematically explore different combinations of hyperparameters to identify the configuration that yields the best performance on a validation set. This process helps to avoid overfitting, a common pitfall in machine learning, where a model performs exceptionally well on the training data but poorly on new, unseen data.
Bias-Variance Tradeoff
A crucial concept in model evaluation is the bias-variance tradeoff. Models with high variance tend to fit the training data very closely, potentially capturing noise and irrelevant details. This can lead to poor generalization performance on unseen data. Models with high bias, on the other hand, tend to be simpler and make strong assumptions about the data, potentially missing important patterns.
The ideal model finds a balance between bias and variance, minimizing both to achieve optimal performance. Finding this balance is often an iterative process, involving experimentation with different model architectures and hyperparameter tuning. Careful consideration of this tradeoff is essential for building robust and reliable machine learning models.
Overfitting and Underfitting
Overfitting and underfitting are two common pitfalls in model building. Overfitting occurs when a model learns the training data too well, including noise and irrelevant details, leading to poor generalization. Underfitting, on the other hand, happens when a model is too simple to capture the underlying patterns in the data, resulting in poor performance on both training and testing sets.
Techniques like regularization help mitigate overfitting by penalizing complex models, and increasing the complexity of the model can address underfitting. Careful evaluation of model performance on both training and testing datasets is essential to identify and address these issues. Understanding the difference between overfitting and underfitting is crucial for building robust models.
Model Comparison and Justification
Comparing different models and justifying the selection of a specific model often involves a comprehensive analysis. This process should consider not only the performance metrics but also the interpretability and maintainability of the model. A model that provides insights into the decision-making process can be beneficial in certain applications, such as healthcare or finance.
The computational cost of training and deploying the model should also be taken into account. A model that is computationally expensive may not be suitable for real-time applications or limited resources. Ultimately, the choice of model should be based on a holistic evaluation considering performance, interpretability, maintainability, and computational cost.